L’algorithme d’Euclide est un outil mathématique permettant de trouver le Plus Grand Commun Diviseur (PGCD) entre deux nombres. Il existe également une évolution nommée Algorithme d’Euclide Étendu afin de trouver les coefficients de Bézout de deux entiers. Tu ne le sais peut-être pas, mais l’algorithme d’Euclide dispose de nombreux avantages dans le secteur informatique, si bien qu’il peut très facilement s’implanter dans le langage Python. Études Tech revient, pour toi, sur cet algorithme.
L’histoire de l’algorithme d’Euclide
L’algorithme d’Euclide est un outil assez puissant qui permet de trouver le Plus Grand Commun Diviseur, appelé PGCD entre deux entiers. La première description de cet algorithme remonte à l’Antiquité grecque lorsque le mathématicien Euclide l’élabore dans son ouvrage « Les Éléments ». La version standard permet de trouver les PGCD, mais il existe une version étendue déterminant les coefficients de Bézout de deux entiers.
Le grand intérêt de l’algorithme d’Euclide, est sa facilité à le prendre en main. Ainsi, il possède de nombreux avantages, notamment en informatique puisqu’il s’implante facilement dans le langage de programmation Python.
L’algorithme d’Euclide standard
Avant de pouvoir réaliser l’algorithme d’Euclide, il faut maîtriser la division euclidienne sur le bout des doigts. C’est pourquoi, nous te faisons un rappel de la manière dont il faut la réaliser.
Quelle est la formule de la division euclidienne ?
La division euclidienne est une méthode de division dans laquelle on divise un nombre (le dividende) par un autre nombre (le diviseur) et on obtient un quotient et un reste. La formule de la division euclidienne est la suivante :
a = bq + r
Ici, « a » est le dividende, « b » est le diviseur, « q » est le quotient et « r » est le reste. Le quotient « q » est le résultat de la division entière de « a » par « b », et le reste « r » est la partie restante qui n’a pas été divisée par « b ». Le reste est toujours un nombre entier compris entre 0 et b-1 inclus.
Par exemple, si on divise 13 par 5, on obtient :
13 = 5 x 2 + 3
Dans cet exemple, le quotient est 2 et le reste est 3.
La formule de la division euclidienne est utilisée dans de nombreux domaines des mathématiques et de l’informatique, notamment pour trouver le PGCD de deux nombres à l’aide de l’algorithme d’Euclide.
Pourquoi l’algorithme d’Euclide donne le PGCD ?
L’algorithme d’Euclide fonctionne en utilisant le fait que si « d » divise à la fois « a » et « b », alors « d » divise aussi leur différence (« a » – « b »). Cela signifie que si « d » est le PGCD de « a » et « b », alors « d » est également le PGCD de « b » et (« a » – « b »). En appliquant cette propriété de manière répétée, l’algorithme d’Euclide cherche le PGCD de « a » et « b » en continuant à diviser « a » par « b », puis « b » par le reste de la division précédente, jusqu’à ce que le reste soit zéro. A ce stade, « b » est le plus grand commun diviseur de « a » et « b ».
Cela fonctionne, car chaque division ne change pas le PGCD de « a » et « b », et finit par produire un reste de zéro, ce qui signifie que « b » divise « a » et donc est un diviseur commun de « a » et « b ». Ainsi, « b » est le plus grand diviseur commun des deux nombres.
En résumé, l’algorithme d’Euclide fonctionne en utilisant la propriété fondamentale selon laquelle le PGCD de deux nombres peut être calculé à partir de leurs différences et en continuant à appliquer cette propriété jusqu’à ce que le reste soit zéro.
Comment calculer le PGCD à l’aide de l’algorithme d’Euclide ?
Comme évoqué plus haut, en utilisant l’algorithme d’Euclide, nous cherchons à déterminer le PGCD de deux entiers. Cela repose sur une suite de division euclidienne dans laquelle a et b sont des entiers. Le principe est le suivant : le PGCD de a et de b est égal à celui de b et du reste de la division.
Mathématiquement, cela peut se représenter par la formule suivante :
PGCD(a, b) = PGCD(b, a mod b).
Prenons un exemple : On cherche le PGCD de 116 et 54.
Dans un premier temps, on divise 116 par 54 ce qui nous donne :
116 = 2×54 + 8 (8 correspondant au reste de la division entre 116 et 54). Ensuite, on prend le précédent diviseur, soit 54 ici, que l’on divise par le reste de la division entre 116 et 54 soit 8, ce qui nous donne :
54 = 6×8+6
On répète la même opération jusqu’à arriver à 0 :
8 (ancien diviseur) = 1×6 (ancien reste) +2
6 = 3×2 0
Le 0 marque la fin de l’algorithme. Une fois arrivé à ce résultat pour trouver le PGCD, on remonte au dernier quotient entier, soit ici 2. Le PGCD de 116 et 54 est donc 2.
L’algorithme d’Euclide étendu
Cette version étendue est une évolution de l’algorithme d’Euclide traditionnel. Ici, l’objectif est de trouver les coefficients de Bézout de deux entiers qui servent à exprimer la résolution de Bézout entre deux entiers. Ces deux coefficients sont u et v. La formule sera la suivante :
PGCD a et b = au – bv
Reprenons l’exemple précédent et trouvons les coefficients de Bézout de 116 et 54.
La première étape consiste à résoudre l’algorithme d’Euclide normalement.
116 = 2×54 + 8
54 = 6×8+6
8 = 1×6 +2
6 = 3×2 + 0
PGCD de 116 et 54 = 2
La formule pour calculer les coefficients de Bézout c’est 2 = 116u – 54v
Pour trouver u et v, il suffit tout simplement de remonter l’algorithme d’Euclide. Dans ce cas, la dernière ligne à savoir : 6 = 3×2 + 0 n’est pas utile et il faut commencer par la ligne précédente, ce qui nous donne :
2 = 8 – 1×6
Et on remonte petit à petit
2 = 8 – 1 (54-6×8)
⬆️
Ligne précédente dans l’algorithme d’Euclide.
Ensuite, on cherche à rassembler les 8 et les 54 :
2 = -1×54 + 7×8
Et on continue de remonter l’algorithme.
2 = -1 x 54 + 7 (116 – 2 x 54)
Dernière étape, comme précédemment, on rassemble les 116 entre eux et les 54 entre eux.
2 = 7×116 – 15×54
L’algorithme est résolu et si on prend la formule précédente à savoir 2 = 116u – 54v alors la résolution est : 2 = 7×116 – 15×54.
Le lien entre l’algorithme d’Euclide et le langage de programmation Python
L’algorithme d’Euclide peut être implanté au sein de Python. Tout d’abord, il va calculer le PGCD de deux entiers, ce qui va prendre la forme suivante :

Ici, la fonction euclidean_algorithm (a,b) correspond au PGCD que Python va devoir trouver. Il lance un boucle while qui ne se termine pas tant que le résultat 0 n’a pas été atteint. À chaque répétition de la boucle, le reste de la division a par b est calculé en utilisant l’opérateur module % et le reste correspond à r. Ensuite, il va mettre à jour les valeurs : a prend la valeur de b et b celle de r, puis on répète l’algorithme jusqu’à trouver les PGCD.
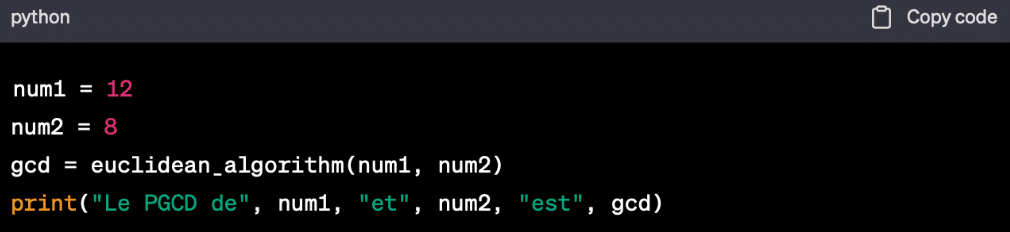

Python peut aussi effectuer l’algorithme d’Euclide étendue de la manière suivante :
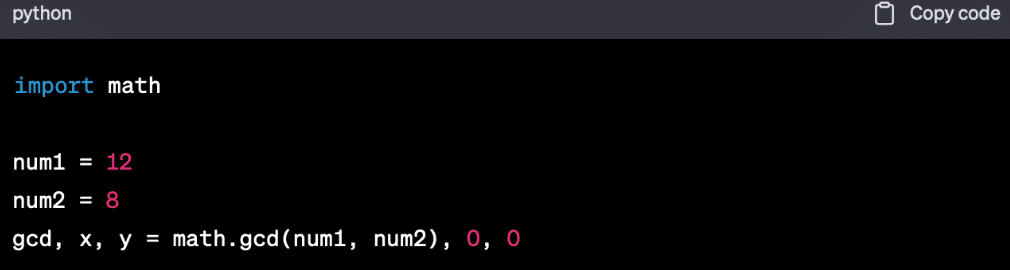
La fonction math.gcd (a, b) utilise l’algorithme d’Euclide étendu pour calculer à la fois le PGCD, mais aussi les coefficients de Bézout. Les valeurs gcd, x et y peuvent servir pour résoudre d’autres problèmes mathématiques. Elle peut également être utilisée pour trouver le PGCD de plusieurs nombres en utilisant une boucle. Le lien entre l’algorithme d’Euclide et le langage de programmation Python est donc étroit, puisque Python fournit une implémentation facile à utiliser et efficace de cet algorithme.
Pour conclure, l’algorithme d’Euclide permet de trouver le PGCD entre deux entiers tandis que l’algorithme d’Euclide étendu cherche les coefficients de Bézout. C’est un outil très pratique en mathématique et en informatique, y compris en cryptographie, dans la théorie des nombres et l’arithmétique modulaire grâce à sa simplicité d’utilisation.
Lire aussi : Guide complet pour apprendre JavaScript






